선형 판별 분석(Linear Discriminant Analysis)
규제가 없는 모델에서 차원의 저주로 인한 과대적합 정도를 줄이고 계산 효율성을 높이기 위한
특성 추출기법으로 사용할 수 있다.
PCA가 데이터셋에 있는 분산이 최대인 직교 서분 축을 찾을려고 하는 반면, LDA의 목표는
클래스를 최적으로 구분할 수 있는 특성 부분 공간을 찾는 것이다.
PCA vs LDA
둘 다 차원 개수를 줄일 수 있는 선형 변환 기법이다. PCA는 비지도 학습 알고리즘이지만,
LDA는 지도 학습 알고리즘이다. 따라서 LDA가 PCA보다 분류 작업에서 더 뛰어난 특성 추출 기법이라고
생각할 수 있다.
(A. M. Martinez는 PCA를 통한 전처리가 특정 이미지 인식 작업에 더 뛰어난 분류 결과를 내는 경향이 있다고
보고 했다. -> 각 클래스에 속한 샘플이 몇 개 되지 않을 때)
LDA는 데이터가 정규 분포라고 가정한다.또한 클래스가 동일한 공분산 행렬을 가지고 훈련 샘플은 서로 통계적으로 독립적이라고 가정한다.
하나 이상의 가정이 조금 위반되더라도 여전히 LDA 차원 축소를 상당히 잘 수행한다.
Process of Linear Discriminant Analysis
1. d 차원의 데이터셋을 표준화 전처리한다.(d는 특성 개수)
2. 각 클래스에 대해 d 차원의 평균 벡터를 계산한다.
3. 클래스 간의 산포 행렬(scatter matrix) S(B)와 클래스 내 산포 행렬 S(W)를 구성한다.
4. S(W)^-1S(B) 행렬의 고유 벡터와 교윳값을 계산한다.
5. 고윳값을 내림차순으로 정렬하여 고유 벡터의 순서를 매긴다.
6. 고윳값이 가장 큰 k개의 고유 벡터를 선택하여 dxk 차원의 변환 행렬 W를 구성한다.
이 행렬의 열이 고유 벡터이다.
7. 변환 행렬 W를 사용하여 샘플을 새로운 특성 부분 공간으로 투영한다.
단계2에서 평균 벡터를 만드는 데 클래스 레이블 정보를 사용(지도 학습)
import pandas as pd
df_wine=pd.read_csv('https://archive.ics.uci.edu/ml/'
'machine-learning-databases/wine/wine.data', header=None)
from sklearn.model_selection import train_test_split
X, y=df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test=\
train_test_split(X,y,test_size=0.3, stratify=y, random_state=0)
from sklearn.preprocessing import StandardScaler
sc=StandardScaler()
X_train_std=sc.fit_transform(X_train)
X_test_std=sc.fit_transform(X_test)
2. 평균 벡터 계산
평균 벡터를 이용하여 클래스 간의 산포 행렬과 클래스 내 산포 행렬을 구성한다.
import numpy as np
np.set_printoptions(precision=4)
mean_vecs=[]
for label in range(1,4):
mean_vecs.append(np.mean(X_train_std[y_train==label], axis=0))
print('MV %s: %s\n' %(label, mean_vecs[label-1]))
MV 1: [ 0.9066 -0.3497 0.3201 -0.7189 0.5056 0.8807 0.9589 -0.5516 0.5416
0.2338 0.5897 0.6563 1.2075]
MV 2: [-0.8749 -0.2848 -0.3735 0.3157 -0.3848 -0.0433 0.0635 -0.0946 0.0703
-0.8286 0.3144 0.3608 -0.7253]
MV 3: [ 0.1992 0.866 0.1682 0.4148 -0.0451 -1.0286 -1.2876 0.8287 -0.7795
0.9649 -1.209 -1.3622 -0.4013]
3. 산포 행렬
클래스 내 산포 행렬(공분산 행렬->아래 설명 참조)
d=13
S_W=np.zeros((d, d))
for label, mv in zip(range(1, 4), mean_vecs):
class_scatter=np.zeros((d, d))
for row in X_train_std[y_train==label]:
row, mv=row.reshape(d,1), mv.reshape(d,1)
class_scatter+=(row-mv).dot((row-mv).T)
S_W+=class_scatter
print('클래스 내의 산포 행렬: %sx%s' %(S_W.shape[0], S_W.shape[1]))
산포 행렬을 계싼할 때 훈련 데이터셋의 클래스 레이블이 균등하게 분포되어 있다고 가정한다.
(클래스 레이블의 개수를 출력해보면 이 가정이 틀렸음을 알 수 있다.)
print('클래스 레이블 분포: %s' %np.bincount(y_train)[1:])
따라서 개별 산포 행렬 S(i)를 산포 행렬 S(W)로 모두 더하기 전에 스케일을 조정해야 한다.
산포 행렬 클래스 샘플 개수 n(i)로 나누면 사실 산포 행렬을 계산하는 것이 공분산 행렬 계산하는 것과
같아진다.
( 공분산 행렬은 산포 행렬의 정규화 )
d=13
S_W=np.zeroes((d, d))
for label, mv in zip(range(1,4), mean_vecs):
class_scatter=np.cov(X_train_std[y_train==label].T)
S_W+=class_scatter
print('스케일 조정된 클래스 내의 산포 행렬: %sx%s' %(S_W.shape[0], S_W.shape[1]))
스케일 조정된 클래스 내의 산포 행렬: 13x13
클래스 간의 산포 행렬
mean_overall=np.mean(X_train_std, axis=0)
mean_overall=mean_overall.reshape(d, 1)
d=13
S_B=np.zeros((d, d))
for i, mean_vec in enumerate(mean_vecs):
n=X_train[y_train==i+1,:].shape[0]
mean_vec=mean_vec.reshape(d,1)
S_B+=n*(mean_vec-mean_overall).dot((mean_vec-mean_overall).T)
print('클래스간의 산포 행렬: %sx%s'%(S_B.shape[0], S_B.shape[1]))
4. 고유 벡터와 고유값
피셔의 LDA를 다중 클래스로 확장한 공식을 라그랑주 승수법(Lagrange multiplier method)를 적용하면,
S(W)^-1S(B)*w=lambda*w
S(W)^-1S(B) 고유값 구하는 문제랑 같다.
eigen_vals, eigen_vecs=\
np.linalg.eig(np.linalg.inv(S_W).dot(S_B))
5. 고유값을 내림차순으로 정렬
eigen_pairs=[(np.abs(eigen_vals[i]), eigen_vecs[:,i]) for i in range(len(eigen_vals))]
eigen_pairs=sorted(eigen_pairs, key=lambda k:k[0], reverse=True)
print('내림차순의 고유값:\n')
for eigen_val in eigen_pairs:
print(eigen_val[0])
내림차순의 고유값:
8.069559874516399
4.123807374708672
7.624087461376092e-16
7.624087461376092e-16
6.413060361030704e-16
6.413060361030704e-16
2.6692482432833378e-16
2.6692482432833378e-16
2.242026826074042e-16
1.8059741847077875e-16
1.512101518595477e-16
9.230804684789262e-17
0.0
LDA에서 선형 판별 벡터는 최대 c-1개 이다. c는 클래스 레이블의 개수
공선성
완벽하게 공선성을 가지는 경우(모든 샘플이 동일 선상에 위치) 공분산 행렬의 랭크는 1이다. 9이 아닌 고유값을
가진 고유벡터가 하나만 만들어진다.
선형 판별 벡터
import matplotlib.pyplot as plt
tot=sum(eigen_vals.real)
discr=[(i/tot) for i in sorted(eigen_vals.real, reverse=True)]
cum_discr=np.cumsum(discr)
plt.bar(range(1, 14), discr, alpha=0.5, align='center', label='Individual "discriminability"')
plt.step(range(1, 14), cum_discr, where='mid', label='Cumulative "discriminability"')
plt.ylabel('"Discriminability" ratio')
plt.xlabel('Linear discriminants')
plt.ylim([-0.1, 1.1])
plt.legend(loc='best')
plt.tight_layout()
plt.show()

처음 2개의 선형 판별 벡터가 Wine 데이터셋에 있는 정보 중 거의 100%를 잡아낸다.
6. dXk 차원의 변환 행렬 W 구성
w=np.hstack((eigen_pairs[0][1][:, np.newaxis].real, eigen_pairs[1][1][:, np.newaxis].real))
print('행렬 W:\n', w)
행렬 W:
[[-0.1585 -0.4078]
[ 0.0982 -0.1817]
[-0.0157 -0.3475]
[ 0.1587 0.3098]
[-0.0206 -0.0644]
[ 0.1885 0.0736]
[-0.7156 0.3031]
[-0.0796 -0.0011]
[ 0.0073 0.0722]
[ 0.3434 -0.2792]
[-0.0255 0.2447]
[-0.3201 -0.0449]
[-0.4053 -0.5809]]
7. 새로운 공간에 투영
X_train_lda=X_train_std.dot(w)
colors=['r', 'b', 'g']
markers=['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
plt.scatter(X_train_lda[y_train==l, 0],
X_train_lda[y_train==l, 1]*(-1),
c=c, label=l, marker=m)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower right')
plt.tight_layout()
plt.show()

세 개의 와인클래스를 새로운 특성 부분 공간에서 선형적으로 완벽하게 구분할 수 있다.
scikit-learn LDA
from sklearn.linear_model import LogisticRegression
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
lda=LDA(n_components=2)
X_train_lda=lda.fit_transform(X_train_std, y_train)
lr=LogisticRegression(random_state=1)
lr=lr.fit(X_train_lda, y_train)
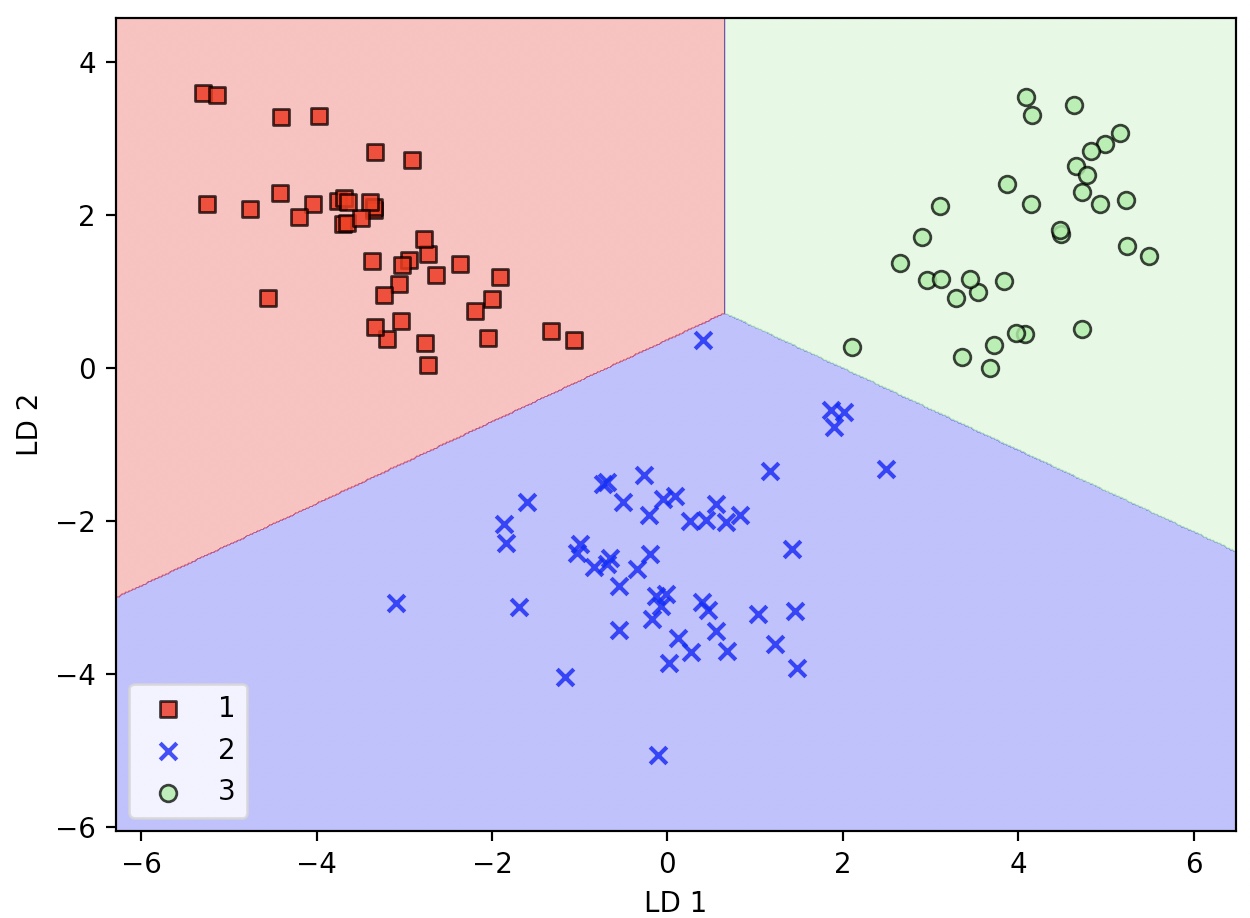
plot_decision_regions(X_train_lda,y_train, classifier=lr)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()
테스트 데이터셋
X_test_lda=lda.transform(X_test_std)
plot_decision_regions(X_test_lda, y_test, classifier=lr)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()

원본 13개의 특성대신 2차원 특성 부분 공간을 이용해서 테스트 데이터셋을 완벽하게 분류
위의 LDA구현은 LinearDiscriminantAnalysis 클래스의 solver 매개변수가 ‘eigen’ 일 때이다.
실제 사이킷런의 LDA 구현은 eigen과 조금 다르다.(default값=‘svd’: 특이값 분해)
svd는 산포 행렬을 직접 계산하지 않기 때문에 특성이 많은 데이터셋에서도 잘 작동한다.
머싱러닝교과서with파이썬, 사이킷런, 텐서플로_개정3판 pg.215
y_uniq, y_count=np.unique(y_train, return_counts=True)
priors=y_count/X_train_std.shape[0]
priors
array([0.3306, 0.4032, 0.2661])
s_w=np.zeros((X_train_std.shape[1], X_train_std.shape[1]))
for i, label in enumerate(y_uniq):
s_w+=priors[i]*np.cov(X_train_std[y_train==label].T, bias=True)
np.cov()함수는 공분산 행렬을 계산할 때, 1/(n-1)을 곱한다.
bias=True로 두면 1/n을 곱한다.
s_b=np.zeros((X_train_std.shape[1], X_train_std.shape[1]))
for i, mean_vec in enumerate(mean_vecs):
n=X_train_std[y_train==i+1].shape[0]
mean_vec=mean_vec.reshape(-1, 1)
s_b+=priors[i]*(mean_vec-mean_overall).dot((mean_vec-mean_overall).T)
S(W)^-1S(B)를 직접구해 교유값 분해를 하는 대신 scipy.linalg.eigh 함수에 직접 S(B) S(W)를 전달해서
고윳값을 계산할 수 있다.
import scipy
ei_val, ei_vec=scipy.linalg.eigh(s_b, s_w)
ei_vec=ei_vec[:, np.argsort(ei_val)[::-1]]
이전의 lda(solver=‘eigen’)에서 lda.covariance_속성을 이용해서 위와 비교할 수 있다.
S(W)(클래스 내 산포 행렬) lda.covariance_속성에 저장
lda_eigen=LDA(solver='eigen')
lda_eigen.fit(X_train_std, y_train)
np.allclose(s_w, lda_eigen.covariance_)
S(B)(클래스 간의 산포 행렬)은 S(T)(총 산포행렬)에서 S(W)(클래스 내 산포 행렬)을 빼서 구할 수 있다.
lda_eigen.scalings 속성에 고유 벡터(선형 판별 벡터) 저장
Sb=np.cov(X_train_std.T, bias=True)-lda_eigen.covariance_
np.allclose(lda_eigen.scalings_[:, :2], ei_vec[:, :2])
True
trainsform 메서드는 단순히 샘플과 고유 벡터의 점곱으로 구할 수 있다.
np.allclose(lda_eigen.transform(X_test_std), np.dot(X_test_std, ei_vec[:,:2]))
True